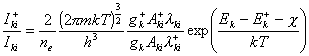
3. Wyznaczanie temperatury ze stosunków natężeń.

                                   

Stosując układ równań (28), (29) oraz równanie Saha-Eggerta otrzymano następującą zależność:

                      

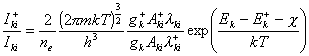
Z tego równania obliczono temperaturę plazmy, która dla stosunku natężeń linii argonowych równego 0,0266  wynosi T=11990K.

 

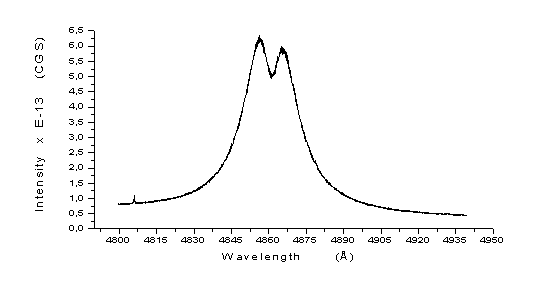 4. Wyznaczanie szerokości połówkowej linii wodorowej H

 

Charakterystyczna linia widmowa wodoru Hb jest przedstawiona na poniższym rysunku:

 

 

 

 
 
 

 

                     

Chcąc dokładnie wyznaczyć szerokość połówkową  tej linii należy uwzględnić "dalekie skrzydła". Aby to zrobić zastosowano następującą formułę:

            

               

gdzie:

        b - stałe widmo ciągłe,

        k - stała,

   y1,y2 -  natężenia odpowiadające odpowiednio początkowi lewego

              "skrzydła" oraz początkowi prawego "skrzydła".

Wykorzystując powyższe  równania wyznaczono wartości k oraz b.

Następnie obliczono natężenia w odległości 150A od początku lewego "skrzydła" linii i w odległości 150A od końca prawego "skrzydła" linii widmowej. Te obliczone wartości pozwoliły na wykreślenie profilu linii widmowej o długości fali l=4861,332A z uwzględnieniem "dalekich skrzydeł" oraz obliczenie szerokości połówkowej, która wynosi  A.

 

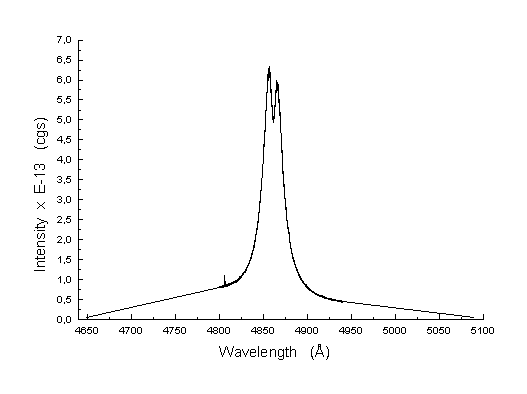
Rys. Linia widmowa wodoru l=4861,332A z dorobionymi "skrzydłami".

 

 5. Wyznaczanie koncentracji elektronów korzystając z szerokości połówkowej linii widmowej atomu wodoru H.

                    

Korzystając z poniższego równania

                       

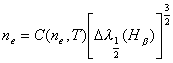
można obliczyć koncentrację elektronów.

Stała C jest funkcją temperatury i koncentracji, mając dane wartości stałej C dla poszczególnych temperatur w przedziale od 5000 K do 40000 K [10]    wyinterpolowano jej wartość odpowiadającą temperaturze 11990 K.

                  Otrzymane wartości stałej C oraz koncentracji elektronów Ne zestawiono w poniższej tabeli:

  (A)   C (Acm-3)         T(K)  Ne (1016 cm-3)
      27,422   3,282*1014       11990       4,713

 

 6. Diagnostyka plazmy.

 

                     Do diagnostyki plazmy zastosowano program komputerowy NFN - 1 autorstwa prof. dr hab. Antoniego Gollego.

Danymi, które zostały wprowadzone do programu diagnostycznego są parametry linii węglowej l=8335,15A, linii tlenowej l=9263,9A; linii argonowej l=4300,101A oraz linii wodorowej Hb  l=4861,332A. Dane te zostały zestawione w poniższej tabeli:

Nazwa pierwiastka l  (A) E(cm)   g   A  (10s) e Dl(A)
Węgiel     CI 8335,15 73975,91 1 0,351 0,029   -----
Tlen         OI 9263,9 97420,75 25 0,419 0,21   -----
Argon      ArI 4300,1 116999 5 0,00394 0,598 0,908
Wodór     HI 4861,33 102798,07 32 0,08419 48,809   -----

Po przeprowadzeniu diagnostyki plazmy otrzymano następujące wartości temperatury i koncentracji składników:

        T=10817 K

       

 7.Wyznaczanie prawdopodobieństw przejść.

                  Korzystając z równania (36) obliczono prawdopodobieństwa przejść przyjmując, że parametry linii widmowej CI l=8335,15A są znane i wynoszą[11]:

   

   

   

   

    (jednostki CGS)

    T=11990 K

Obliczono prawdopodobieństwa przejść Aki, które zostały zamieszczone w tabeli:

       Przejście      l(A)     E(cm-1)    g    Aki(108s-1)

 

      D
  3p 3D  - 5s 3P0   7116,99     83791,04    5 0,10   0,03     D
  3s 1P0  - 3p 1S   8335,15     73975,91    1 0,35   0,02     A
 

 

  3s 3P0 - 3p 3P

   9061,44     71385,38    5 0,065 0,005     A
  9062,49     71364,9    3 0,083 0,007     A
  9078,29     71364,9    3 0,07   0,01     C
  9088,51     71352,51    1 0,26   0,02     A
  9094,83     71385,38    5 0,20   0,02     A
  3s 1P0 - 3p 1D   9405,73     72610,72    5 0,26   0,02     A
  3s 3P0 - 3p  3S   9620,78     70743,95    3 0,014 0,002     B

Tabela 2: Zestawienie wartości obliczonych prawdopodobieństw przejść.

                  Oszacowano dokładności pomiaru Aki i w rubryce " D" stosowano kod literowy dla wartości błędu:

                 A < 10%

     10%  B  15%

     15% < C < 20%

     20%  D 30% 

 8. Wyznaczanie parametrów starkowskich wybranych linii widmowych CI.

                    Korzystając z danych tablicowych [10] wyinterpolowano wartości parametrów: w, a(w - parametr szerokości połówkowej, a - parametr asymetrii linii). Następnie policzono wartości współczynnika wtot dla profilu Lorentza z zależności:

        

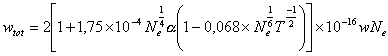
dla wybranych długości fal[12].

  

     Typ         przejścia    l (A)   w(A)       a   T(K) N(cm-3) w(A) w(A)
3s 1P0 - 3p  1S  8335,2 0,127  0,043 11990      4,713   1,197 1,081
3s 3P0 - 3p  3P  9088,5 0,082  0,027 11990      4,713   0,773 0,803
 3s 3P0 - 3p 3S  9620,78 0,072  0,017 11990      4,713   0,679 0,774

Tabela 3: Zestawienie parametrów starkowskich dla tych długości fal, dla

                  których były dane wartości tablicowe.

Zestawienie wartości parametrów przesunięcia linii (shift) przedstawia poniższa tabela:

Wzorzec (A) Plazma (A) Shift (A)
        7116,99          7117,44           0,45
        8335,15          8335,52           0,37
        9061,44          9061,05           0,39
        9062,49          9062,53           0,04
        9078,29          9077,82           0,47
        9088,51          9089,00           0,49
        9094,83          9094,85           0,02
        9405,73          9405,68           0,05
        9620,78          9621,65           0,87

 

VI. Porównanie wyników eksperymentalnych z danymi literaturowymi.

 

                  Zestawienie prawdopodobieństw przejść otrzymanych w tym eksperymencie z danymi literaturowymi przedstawia poniższa tabela.

     Przejście      l(A)    E(cm-1)   g   Aki (108s-1)

(1)

    Aki (108s-1)

(2)

    Aki (108s-1)

       [11]

    Aki(108s-1)

       [13]

  Aki(108s-1)

       [8]
   3p 3D - 5s 3P0   7116,99    83791,04    5 0,09  0,03 0,10   0,03        0,0326         ---        ---
   3s 1P0 - 3p 1S   8335,15    73975,91    1 0,35  0,02 0,35   0,02        0,351        0,32      0,301
 

 

   3s 3P0 - 3p 3P

   9061,44    71385,38    5 0,07  0,01 0,065 0,005        0,0731        0,065        ---
  9062,49    71364,9    3 0,0850,008 0,083 0,007        0,0948        0,083        ---
  9078,29    71364,9    3 0,0810,009 0,07   0,01        0,0707        0,062        ---
  9088,51    71352,51    1 0,27  0,02 0,26   0,02        0,3        0,25        ---
  9094,83    71385,38    5 0,21  0,02 0,20   0,02        0,228        0,19        ---
   3s 1P0 - 3p 1D   9405,73    72610,72    5 0,26 0,02 0,26   0,02        0,291        0,13       0,159
   3s 3P0 - 3p 3S   9620,78    70743,95    3 0,0140,002 0,014 0,002        0,0862        0,074        ---

 (1)- prawdopodobieństwa przejść wyznaczone z wykorzystaniem temperatury T=10819K, otrzymanej z diagnostyki plazmy przy zastosowaniu programu komputerowego NFN - 1.

(2)- prawdopodobieństwa przejść wyznaczone z wykorzystaniem temperatury T=11990K, otrzymanej ze stosunku natężeń linii argonowych IArII/IArI.

 

VII. Wnioski.

                  Celem tej pracy było badanie widma węgla neutralnego w bliskiej podczerwieni. W pierwszej kolejności zbadano samoabsorpcję plazmy. W tym celu policzono stosunek natężenia w maksimum każdego profilu do funkcji Plancka, stosunek ten nie przekraczał 0,4% więc zaniedbano wpływ samoabsorpcji na dalsze wyniki eksperymentu.

Po przeprowadzeniu diagnostyki plazmy  wykorzystując program komputerowy NFN - 1 otrzymano wartość temperatury i koncentracji. Ponadto wyznaczono temperaturę ze stosunku natężeń linii argonu w dwóch różnych stanach jonizacyjnych, a koncentrację elektronów z szerokości połówkowej linii Hb. Różnice w wyznaczeniu tych dwóch parametrów różnymi metodami są następujące: DT=1171 K, a DNe=0,2041016 cm-3. Wartość temperatury do dalszych obliczeń wzięto z drugiej metody ponieważ jest ona dokładniejsza, gdyż wszystkie błędy systematyczne związane z niepewnością w pomiarze długości słupa plazmy i absolutnej kalibracji natężenia znikają.

                  Obliczone w tej pracy wartości prawdopodobieństw przejść zamieszczono w tabeli 2. Jak widać wszystkie obliczone wartości są porównywalne z wartościami tablicowymi [11], tylko prawdopodobieństwo przejścia dla linii o długościach fal l=7116,99 A i l=9620,78 A znacznie odbiegają od wartości tablicowych.

                  Obliczono również teoretyczne wartości szerokości połówkowych niektórych linii widmowych oraz porównano je z wartościami zmierzonymi. Jak widać wartości te zgadzają się z wartościami zmierzonymi w eksperymencie.

                  W ostatniej części analizy eksperymentu wzięto pod uwagę shift, czyli przesunięcie linii otrzymanych z analizy promieniowania plazmy w stosunku do linii wzorcowych.

                  Każdy otrzymany profil linii widmowej węgla neutralnego w postaci punktów pomiarowych był przybliżany w programie Origin 4.1 profilem Lorentza. W związku z tym wiąże się pewna niedokładność dopasowania, która nie zależy od eksperymentatora, a wpływa na większość otrzymanych w eksperymencie wyników.

 

VIII. Literatura.

 

 

1.   Z. Leś, Wstęp do spektroskopii atomowej, Warszawa 1969.

2.   D. Kunisz, Fizyczne podstawy emisyjnej analizy widmowej, Warszawa 1973.

3.     A. Kordus, Plazma, Warszawa 1985.

4.   T. Wujec, Wyznaczanie prawdopodobieństw przejść dla wybranych linii argonu, Zeszyty Naukowe WSP w Opolu (1972) Fizyka XIII.

5.   A. Golly, Diagnostyka termicznej i optycznie cienkiej plazmy argonowo - węglowo - tlenowej, Zeszyty Naukowe WSP w Opolu (1972) Fizyka XIII.

6.   T. Wujec, Wyznaczanie prawdopodobieństw przejść dla linii argonu I i II, Zeszyty Naukowe (1973) Fizyka XV.

7.   H.W. Drawin, Ergebnisse der Plasmaphysik und der Gaselektronik 3, Akademie - Verlag Berlin (1972).

8.   A. Golly, Wyznaczanie prawdopodobieństw przejść dla niektórych astrofizycznie ważnych atomów i jonów, Studia i monografie nr 129, Opole 1986.

9.   B. Grabowski, T. Wujec, Profile linii widmowych II, Teoretyczne i doświadczalne profile linii argonu, Zeszyty Naukowe WSP w Opolu (1969) Fizyka X.

10. H. Griem, Plasma spectroscopy, New York 1964.

11. W.L. Wiese, J.R. Fuhr, T.M. Deters, Atomic transition probabilities of carbon, nitrogen and oxygen a critical data compilation, USA 1996.

12. S. Djurović, R. Konjević, M. Platiša and N.Konjević, J. Phys. B: At. Mol. Opt. Phys 21, 739 - 748 (1988).

13. W.L. Wiese, M.W. Smith, B.M. Glennon, Atomic transition probabilities, NBS - 4, 1, Washington 1966.

14. Z. Celiński, Plazma, Warszawa 1980.

Wszelkie prawa zastrzeżone.
Kopiowanie, powielanie i wykorzystywanie części lub całości informacji zawartych na tych stronach bez zgody autora zabronione.

Wstecz