UNIWERSYTET OPOLSKI

WYDZIAŁ MATEMATYKI FIZYKI I CHEMII

INSTYTUT FIZYKI

Jarosław Tomczyk

BADANIE WIDMA WĘGLA W BLISKIEJ PODCZERWIENI

Praca magisterska

wykonana pod kierunkiem

prof. dr hab. Antoniego Gollego

Opole 1999

Spis treści.

I. Wprowadzenie................................................................................................................................................5

II.Widma............................................................................................................................................................7

1.Widma optyczne..............................................................................................................................................7

1.1.Widma liniowe............................................................................................................................................. 7

1.2.Widma pasmowe......................................................................................................................................... 8

1.3.Widma ciągłe................................................................................................................................................8

2.Widma emisyjne i absorpcyjne........................................................................................................................ 8.

III. Plazma.........................................................................................................................................................10

1.Promieniowanie plazmy.................................................................................................................................. 11

1.1. Natężenie linii spektralnej............................................................................................................................11

1.2.Plazma termiczna.........................................................................................................................................12

2. Modele równowagi termodynamicznej w plazmie.......................................................................................... 13

2.1. Model pełnej równowagi termodynamicznej............................................................................................... 13

2.2. Model lokalnej równowagi termodynamicznej.............................................................................................14

2.3. Model częściowej lokalnej równowagi termodynamicznej...........................................................................15

3. Prawa opisujące własności plazmy w modelu LRT....................................................................................... 16

3.1. Prawo Daltona wraz z równaniem stanu gazu doskonałego.........................................................................16

3.2. Warunek quasi-neutralności plazmy.......................................................................................................... 16

3.3. Prawo Saha-Eggerta.................................................................................................................................17

3.4. Prawo Maxwella..................................................................................................................................... 18

3.5. Prawo Boltzmanna.................................................................................................................................. 18

4. Diagnostyka plazmy w modelu LRT.............................................................................................................19

4.1. Wyznaczanie temperatury i koncentracji elektronów.................................................................................22

5. Parametry określające przejścia elektronów w atomie..................................................................................24

5.1. Prawdopodobieństwa przejść. Czas życia stanów wzbudzonych.............................................................. 24

5.2. Wyznaczanie prawdopodobieństw przejść metodą natężeniową................................................................ 26

6. Profile linii widmowych.................................................................................................................................27

6.1. Profil Lorentza..........................................................................................................................................27

IV. Opis eksperymentu....................................................................................................................................29

1. Schemat układu pomiarowego......................................................................................................................29

1.1. Kaskadowy palnik plazmowy jako źródło promieniowania elektromagnetycznego......................................30

1.2. Spektrograf, OMA - 4..............................................................................................................................31

1.3.Układ optyczny, rejestracja widma.............................................................................................................32

V. Opracowanie wyników eksperymentu......................................................................................................... 34

1. Wstępne opracowanie plików zawierających badane widma......................................................................... 34

2. Sprawdzenie samoabsorpcji...........................................................................................................................41

3. Wyznaczanie temperatury ze stosunków natężeń.............................................................................................41

4. Wyznaczanie szerokości połówkowej linii wodorowej H............................................................................. 42

5. Wyznaczanie koncentracji elektronów korzystając z szerokości połówkowej linii widmowej atomu wodoru H 43

6. Diagnostyka plazmy.......................................................................................................................................44

7.Wyznaczanie prawdopodobieństw przejść.......................................................................................................45

8. Wyznaczanie parametrów starkowskich wybranych linii widmowych CI..........................................................46

VI. Porównanie wyników eksperymentalnych z danymi   literaturowymi............................................................. 47

VII. Wnioski.................................................................................................................................................... 48

VIII. Literatura..................................................................................................................................................50

I. Wprowadzenie.

                 Badanie widm znane jest pod nazwą analizy spektralnej i opiera się na fakcie, że skoro każdy pierwiastek wysyła charakterystyczne dla siebie widmo, to możliwe jest także postępowanie odwrotne, a więc na podstawie danego widma można wnioskować o składzie chemicznym substancji która jest za to widmo odpowiedzialna. Dzięki temu, że metoda analizy spektralnej jest stosunkowo prosta i szybka w zastosowaniu oraz bardzo czuła (tak, że przy jej pomocy można wykryć nadzwyczaj małe ilości poszczególnych pierwiastków) znalazła szerokie zastosowanie w wielu gałęziach nauki i techniki.

                 Jedną z podstawowych własności plazmy jest to, że wysyła promieniowanie elektromagnetyczne w szerokim zakresie częstości. To promieniowanie niesie informację o warunkach fizycznych w źródle plazmy i może być wykorzystane do wyznaczenia jej parametrów. Diagnostykę plazmy przeprowadza się często na podstawie natężeń i szerokości połówkowych linii widmowych. Natężenie I_ki emisyjnej linii widmowej zależy od parametrów plazmy i od wartości prawdopodobieństwa A_ki emisji spontanicznej atomu przy przejściu z poziomu k na poziom i.

                  Celem tej pracy jest wyznaczenie koncentracji elektronów, przesunięcia (shiftu), szerokości połówkowych badanych linii widmowych oraz wartości prawdopodobieństw przejść, których znajomość jest podstawą interpretacji widm atmosfer gwiazdowych, gdyż zasadniczym źródłem informacji o danym ciele niebieskim jest dochodzące do nas promieniowanie. Wartości prawdopodobieństw przejść są interesujące dla badaczy przestrzeni kosmicznej i górnych warstw atmosfery, w próbach fuzji termojądrowej, są również podstawą rozwoju systemów laserowych. Oprócz zastosowań praktycznych bardzo istotny jest wzgląd czysto poznawczy ponieważ prawdopodobieństwa przejść mogą bowiem informować o strukturze powłoki elektronowej i typie oddziaływań między elektronami.

                 Źródłem plazmy której światło poddane zostało analizie był łuk elektryczny wytworzony w atmosferze argonu z domieszką ódłem plazmy, której światło dwutlenku węgla oraz wodoru. Łuk elektryczny został wytworzony we wnętrzu specjalnej konstrukcji palniku plazmowym. Zasadniczymi elementami zestawu doświadczalnego oprócz palnika plazmowego były: spektrograf siatkowy PGS - 2, wielokanałowy analizator optyczny OMA - 4 oraz komputer.

II.  Widma.

                 Dla każdej substancji istnieją pewne, ściśle określone częstości fal elektromagnetycznych, które w odpowiednich warunkach jest ona w stanie wyemitować lub zaabsorbować, zbiór wszystkich tego typu fal stanowi widmo rozważanej substancji.

 1.Widma optyczne.

                 Mówiąc o widmach atomowych bardzo często ma się na myśli jedynie optyczne widma atomowe, które powstają w wyniku zmiany energii najbardziej zewnętrznych elektronów w atomie. Ze względu na zakres długości fal, które wchodzą w skład tego typu widma dzielimy je na widmo widzialne (od około 7500A do około 4000A), widmo podczerwone, którym zajmowano         się w tej pracy (od długofalowej granicy obszaru widzialnego w stronę fal dłuższych) i widmo nadfioletowe (od krótkofalowej granicy obszaru widzialnego w stronę fal krótszych). W tym zakresie długości fal w którym występują widma optyczne, obserwuje się trzy zasadniczo różne typy widm: widma liniowe, pasmowe i ciągłe.

   1.1.Widma liniowe. 

                  Za widma liniowe odpowiedzialne są głównie atomy lub jony swobodne. Widma te składają się z szeregu linii spektralnych, spośród których dają się wydzielić tzw. serie widmowe czyli grupy linii charakteryzujących się tym, że ich natężenia i wzajemne odległości maleją w miarę jak przechodzimy do fal coraz krótszych.

 1.2.Widma pasmowe.

                  Za widma pasmowe odpowiedzialne są molekuły lub ich jony. Widma te również składają się z poszczególnych linii, jednak ogólna struktura tych widm jest wyraźnie inna niż struktura widm liniowych, gdyż nie mają one charakteru seryjnego. W najbardziej typowej postaci widm pasmowych linie wchodzące w ich skład są w pewnych obszarach tak zagęszczone, że przy obserwacji przyrządami spektralnymi o niezbyt wysokiej zdolności rozdzielczej zlewają się, tworząc w ten sposób charakterystyczne "pasma".

   1.3.Widma ciągłe.

                  Za widma ciągłe odpowiedzialne są przede wszystkim układy skondensowane (kryształy, ciała bezpostaciowe, ciecze, gazy pod bardzo dużymi ciśnieniami), znajdujące się w odpowiednio wysokiej temperaturze. Bardzo często widma tego typu nie są charakterystyczne, tzn. za pomocą analizy spektralnej nie można ustalić składu substancji, która brała udział w powstaniu tego widma. Rozkład natężeń w widmie ciągłym zależy w sposób istotny od temperatury.

 2.Widma emisyjne i absorpcyjne.

                 Widmo emisyjne jest to rozkład promieniowania wysyłanego przez substancję, która w pewien sposób została uprzednio wzbudzona, tzn. że wchodzące w jej skład atomy lub molekuły zostały przeniesione do wyższych stanów energetycznych. Stosuje się różne metody wzbudzania w zależności od cech charakterystycznych danej substancji i cech szczegółowych widma, które chcemy otrzymać. Wszystkie te metody dzieli się zazwyczaj na dwie grupy: wzbudzenie termiczne i wzbudzenie luminescencyjne.

                  W przypadku wzbudzenia termicznego energia potrzebna do wzbudzenia powstaje wyłącznie kosztem energii kinetycznej ruchu cieplnego zderzających się cząstek. Takim źródłem jest np. palnik plazmowy. Wzbudzenie termiczne ma tę zaletę, że jedynie dla źródeł tego typu można założyć równowagę termodynamiczną, tzn. przyjąć, że zależność liczby atomów (lub innych cząstek) w poszczególnych stanach energetycznych od energii tych stanów jest zgodna z prawem Maxwella-Boltzmanna.Wzbudzenie wszelkiego innego rodzaju, które powstaje nie wyłącznie kosztem energii termicznej nazywamy wzbudzeniem luminescencyjnym.

                  Widmo absorpcyjne otrzymuje się wówczas, gdy światło o widmie ciągłym przechodzi przez warstwę substancji, która pochłania fale elektromagnetyczne o charakterystycznych dla siebie częstościach. Absorpcja zachodzi tym intensywniej im warstwa badanej substancji jest grubsza, a ciśnienie większe. Podobnie jak w przypadku widma emisyjnego, widmo absorpcyjne atomów ma strukturę liniową, a widmo molekuł-pasmową[1]. 

III. Plazma.

                 Każda substancja w odpowiednio wysokiej temperaturze może przejść w stan plazmy w wyniku jonizacji przede wszystkim cieplnej. Przyczyny i sposoby prowadzące do jonizacji mogą być następujące:   

.        jonizacja zderzeniowa występująca pod wpływem pola elektrycznego,

.        fotojonizacja związana ze zjawiskiem promieniowania,

.        jonizacja powierzchniowa (emisja) związana z podgrzaniem materiału elektrod.

Jest wiele definicji plazmy, a ja przytoczę tutaj jedną z nich. Plazmą nazywamy stan materii złożony z elektronów, atomów, jonów i ewentualnie, w przypadku plazmy niskotemperaturowej, z molekuł, o ile układ tych cząstek jako całość jest elektrycznie obojętny, czyli suma ładunków ujemnych jest równa sumie ładunków dodatnich [2].

Natura plazmy zależy od rodzaju użytego gazu, jego ciśnienia i energii. Plazma jest podstawowym składnikiem Wszechświata, gdyż większa część materii znajduje się w stanie plazmy. Z plazmy są zbudowane gwiazdy, mgławice, materia międzygwiezdna. Jest ona normalnym stanem skupienia materii w wysokich temperaturach, powyżej 10000K lub w stanach silnego rozrzedzenia i istnienia fal elektromagnetycznych. Naturalne występowanie plazmy na Ziemi jest bardzo rzadkie, nad Ziemią plazma jest przechwytywana przez ziemskie pole magnetyczne w warunkach niemal próżniowych. W jonosferze plazma powstaje na skutek fotojonizacji rzadkiej tam atmosfery. Występuje również w zorzy polarnej i wyładowaniach atmosferycznych.

Najczęściej w warunkach ziemskich plazma jest wytwarzana w laboratoriach lub różnych urządzeniach technicznych np. procesy wyładowań w rozrzedzonych gazach (rury fluorescencyjne), wyładowania łukowe, reaktory termonuklearne [3].

 1.Promieniowanie plazmy.

                  Plazma jest źródłem promieniowania elektromagnetycznego liniowego oraz ciągłego. Promieniowanie liniowe powstaje w wyniku elektronowych przejść między dyskretnymi stanami energetycznymi atomu, a ciągłe na skutek przejść ze stanów swobodnych do swobodnych oraz ze stanów swobodnych do związanych (dyskretnych) [4].

     1.1. Natężenie linii spektralnej.

                  Dla scharakteryzowania wielkości promieniowania liniowego wprowadzono pojęcie współczynnika spontanicznej emisji linii widmowej e. Definiuje się go jako ilość energii wypromieniowanej przez jednostkę objętości plazmy w jednostkowy kąt bryłowy w jednostce czasu przy promienistym przejściu atomów ze stanu wyższego (k-tego) do niższego (i-tego).

                                               (1)

 - prawdopodobieństwo spontanicznego przejścia elektronów z górnego

         stanu k na dolny i,

 -  koncentracja atomów lub jonów wzbudzonych do górnego poziomu k,

  - energie emitowanych kwantów.

                  Dla plazmy znajdującej się w lokalnej równowadze termodynamicznej (LRT) koncentracje wzbudzonych atomów lub jonów do k-tego poziomu można określić z prawa Boltzmanna. Współczynnik emisji linii widmowej można wtedy wyrazić równaniem:

                                               (2)

 -  koncentracja atomów,

 - suma stanów atomu,

  - temperatura,

 - waga statystyczna k-tego poziomu,

 - energia k-tego poziomu [4].

  1.2.Plazma termiczna.

                 Plazmę, w której zachodzi detaliczna równowaga wszelkich procesów wzbudzenia i jonizacji z procesami utraty energii przez atomy oraz  procesami rekombinacji i w której można określić jedną wspólna temperaturę dla wszystkich składników, nazywa się plazmą termiczną.

                 Plazma ta ma tę właściwość, że wszystkie stałe równowagi, średnie prędkości cząstek, przewodnictwo elektryczne i cieplne, promieniowanie, itp. są jednoznacznymi funkcjami temperatury (przy ustalonym ciśnieniu całkowitym). Nie przyjmuje się jednej wartości temperatury dla całego słupa plazmy łukowej lecz jej rozkład, co sprawia, że nie występuje wtedy zupełna równowaga termodynamiczna w całej objętości rozpatrywanej plazmy. Okazuje się, że nie jest to warunek konieczny i wystarczy tzw. lokalna równowaga termodynamiczna czyli muszą istnieć dowolnie małe obszary, w których ustalają się quasistacjonarne rozkłady stanów energetycznych, odpowiadające określonej temperaturze.

                  W plazmie nie znajdującej się w równowadze termodynamicznej temperatury kinetyczne poszczególnych składników mogą być diametralnie różne i jest to wtedy plazma nietermiczna [5]. 

 2. Modele równowagi termodynamicznej w plazmie.

      2.1. Model pełnej równowagi termodynamicznej.  

                  Warunkiem koniecznym i wystarczającym wystąpienia pełnej równowagi termodynamicznej jest wystąpienie równowagi detalicznej. Oznacza to, że w jednostce czasu występuje taka sama liczba danych procesów w plazmie co i procesów do nich przeciwnych (np. identyczna musi być liczba aktów jonizacji co i rekombinacji).

                  Plazma w modelu pełnej równowagi termodynamicznej jest określona przez cztery podstawowe prawa:

.        Maxwella  -   określające rozkład prędkości cząstek,

.        Boltzmanna -  podające rozkład energii wewnętrznej cząstek,

.          Saha-Eggerta - oznaczające stopień jonizacji w plazmie,

.        Plancka - wyznaczające gęstość energii promieniowania w plazmie.

W tym momencie skupię się tylko na opisaniu prawa Plancka ponieważ nie będzie  ono brane pod uwagę przy diagnostyce plazmy.

              Prawo Plancka podaje gęstość promieniowania plazmy zrównoważonej, którą można wyrazić za pomocą równania:

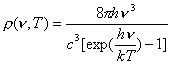
                                               (3)

które w funkcji długości fali przyjmuje postać:

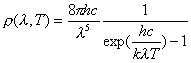                                                (4)

gdzie:

- gęstość promieniowania plazmy,

  -  prędkość światła w próżni,

       -  stała Plancka,

  -  stała Boltzmanna,

 - długość fali.      

                  Dla wszystkich praw obowiązuje taka sama temperatura. Plazma taka występuje jedynie we wnętrzach gwiazd i w jądrze eksplozji nuklearnej[2].

 2.2. Model lokalnej równowagi termodynamicznej.

                Stan równowagi termodynamicznej w plazmie ustala się w wyniku zderzeń atomów i elektronów oraz emisji i absorpcji promieniowania.

                  Stan lokalnej równowagi termodynamicznej(LRT) polega na tym, że w elemencie objętości d układu ustala się pewna temperatura T(x,y,z).

                  Plazma pozostająca w stanie lokalnej równowagi termodynamicznej charakteryzuje się następująco:

a)     rozkładem obsadzenia poszczególnych poziomów energetycznych  każdego   rodzaju atomów, jonów, molekuł i rodników spełniających prawo  Boltzmanna,

b)    stopniem jonizacji każdego typu molekuł, rodników, atomów spełniających prawo Saha-Eggerta,

c)     dysocjacją molekuł i rodników zgodną z równaniem równowagi chemicznej.

                 Różnica stanu lokalnej równowagi termodynamicznej w stosunku do równowagi termodynamicznej polega na tym, że rozkład gęstości promieniowania nie jest zgodny z prawem Plancka, ponieważ emisja i absorpcja promieniowania odgrywa w tym przypadku bardzo małą rolę w procesie ustalania się równowagi[2].

 2.3. Model częściowej lokalnej równowagi termodynamicznej.

                     Model częściowej lokalnej równowagi termodynamicznej(CLRT) plazmy został zaproponowany przez Drawina.

Model ten nieznacznie różni się od modelu lokalnej równowagi termodynamicznej. Wszystkie prawa słuszne dla stanu LRT spełnione są w modelu częściowej lokalnej równowagi termodynamicznej z pewnymi odstępstwami. Dla tego modelu prawo Boltzmanna nie opisuje obsadzenia wszystkich poziomów energetycznych. Prawo Boltzmanna spełnione jest tylko dla stanów wzbudzonych. Zgodnie z tym modelem, liczba atomów w stanie podstawowym jest większa od liczby, jaką uzyskuje się z prawa Boltzmanna na podstawie znajomości temperatury i obsadzenia poziomów wzbudzenia. Nadmierne obsadzenie stanów wzbudzonych atomów w plazmie, zwane nadpopulacją poziomu podstawowego, oznacza odstępstwo od stanu równowagi termodynamicznej pomiędzy stanami podstawowymi atomów a ich stanami wzbudzonymi. Model częściowej równowagi termodynamicznej przewiduje między innymi modyfikację prawa Boltzmanna polegającą na wprowadzeniu do tego prawa wielkości "b" zwanej współczynnikiem nadpopulacji, którą można uważać za miarę odstępstwa od stanu lokalnej równowagi termodynamicznej. Prawo Boltzmanna obowiązujące w modelu częściowej lokalnej równowagi termodynamicznej można zapisać w postaci :

               =                           (5)                                 

gdzie:

  - koncentracja atomów w stanie k-tym,

 - koncentracja atomów w stanie podstawowym,

 - waga statystyczna poziomu podstawowego,

 - waga statystyczna poziomu górnego,

 - energia górnego poziomu,

 - koncentracja elektronów,

 - stała Boltzmanna.

Wielkość b jest dla ustalonego rodzaju atomu lub jonu skomplikowaną funkcją koncentracji elektronów i temperatury. 

 3. Prawa opisujące własności plazmy w modelu LRT.

3.1. Prawo Daltona wraz z równaniem stanu gazu doskonałego.

                  Ponieważ plazma jest mieszaniną wielu składników, więc całkowite ciśnienie plazmy jest sumą ciśnień cząstkowych (parcjalnych) tj. takich jakie występowałyby, gdyby dany składnik plazmy zajmował całą objętość.

                                                (6)

     - ciśnienie całkowite plazmy,

     - koncentracje składników plazmy,

    k- stała Boltzmanna,

   T- temperatura bezwzględna.

3.2. Warunek quasi-neutralności plazmy.

                Neutralność elektryczna jest jedną z podstawowych cech stanu plazmowego. Oznacza ona, że w jednostce objętości plazmy znajduje się taka sama liczba ładunków ujemnych jak i dodatnich i plazma dla zewnętrznego obserwatora jest ośrodkiem elektrycznie neutralnym. Warunek ten nie jest jednak ściśle spełniony, możliwe jest powstawanie w plazmie niewielkich zakłóceń neutralności zarówno w przestrzeni, jak i w czasie. Dlatego też mówi się o plazmie, że jest quasi-neutralna.

                                               (7)

gdzie:

- koncentracja elektronów,

- koncentracje jonów.

3.3. Prawo Saha-Eggerta.

Prawo Saha-Eggerta określa stopień jonizacji plazmy zrównoważonej w zależności od temperatury tj. udział elektronów w ogólnej liczbie cząstek gazu, określa temperatura gazu. W celu wyprowadzenia prawa Saha-Eggerta wykorzystuje się fakt , że w układzie zrównoważonym szybkość jonizacji jest równa szybkości rekombinacji jonów, co prowadzi do wyrażenia na stałą równowagi określającą stopień jonizacji:

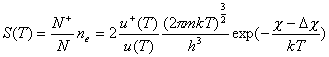                                      (8)

gdzie:

        - koncentracja jonów,

       N  -  koncentracja atomów,

   - sumy stanów odpowiednio dla jonów i atomów,

h-  stała Plancka ,

             - energia jonizacji atomów,

           - obniżenie energii jonizacji na skutek zaburzenia poziomów

                   energetycznych atomu lub jonu w polu elektrycznym plazmy.

3.4. Prawo Maxwella.

Plazma zrównoważona charakteryzuje się pewnym stałym w czasie, zależnym od temperatury, rozkładem prędkości cząstek wyznaczonym przez prawo Maxwella:

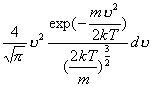                                              (9)

  - całkowita liczba cząstek danego składnika plazmy,

 - liczba cząstek tego składnika, których wartości prędkości znajdują się w

           przedziale (,

  - masa cząstki danego składnika,

      - stała Boltzmanna,

     - temperatura bezwzględna,

    - prędkość cząstki.

W plazmie zrównoważonej wszystkie rodzaje cząstek; atomy, elektrony, jony, itd. mają tę samą średnią energię kinetyczną, a więc można im przypisać tę samą temperaturę. W tym sensie plazmę zrównoważaną nazywamy izotermiczną.

3.5. Prawo Boltzmanna.

Prawo Boltzmanna podaje rozkład cząstek danego rodzaju, np. atomów określonego pierwiastka, na poszczególne stany kwantowe charakteryzujące się różną energią wewnętrzną. Wynika ona z praw kwantowej fizyki statystycznej przy założeniu, że energia oddziaływania cząstek jest znacznie mniejsza od ich energii kinetycznej lub, co na jedno wychodzi, że czas oddziaływania jest znacznie krótszy od czasu swobodnego przelotu.

            Jeżeli przez N oznaczymy ogólną liczbę identycznych atomów w 1cm, mogących występować w stanach kwantowych  a przez  odpowiednio koncentracje atomów w tych stanach, to zgodnie z prawem Boltzmanna, liczba atomów wzbudzonych do i-tego stanu  wiąże się z liczbą atomów znajdujących się w podstawowym stanie energetycznym  oraz z całkowitą liczbą atomów równaniami:

                                                                     (10)

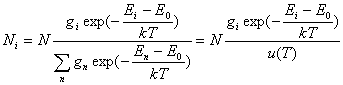                              (11)

gdzie  są wagami statystycznymi poziomów odpowiednio wyższego i podstawowego, a sumowanie przeprowadzono po wszystkich stanach kwantowych danego atomu[2].

 4. Diagnostyka plazmy w modelu LRT.

                  Spektroskopia plazmy należy do najczęściej używanych metod diagnostycznych plazmy. Ogromną jej zaletą jest nie wprowadzanie zakłóceń do plazmy w czasie pomiarów. Metody spektralne pozwalają określić niektóre właściwości plazmy na podstawie szczegółowej analizy składu i charakteru emitowanego przez plazmę promieniowania elektromagnetycznego.

                  Ponieważ emitowane przez plazmę promieniowanie powstaje w wyniku procesów elementarnych zachodzących w plazmie niesie ono z sobą zasób informacji o parametrach plazmy, takich jak jej skład, koncentracja i temperatura elektronów, gęstość i temperatury innych składników plazmy, wartości pól elektrycznych i magnetycznych,  przewodnictwo elektryczne, ciśnienie statyczne i dynamiczne, strumień entalpii, prędkość przepływu plazmy.

W tej pracy pojęcie diagnostyki plazmy jest zawężone do określenia jej temperatury i koncentracji składników.

                  Diagnostykę plazmy przeprowadza się przy założeniu, że:

O     w plazmie nie zachodzi samoabsorpcja promieniowania, czyli może być uważana za optycznie cienką,

O     plazma znajduje się w LRT, tzn. można stosować do niej prawo Boltzmanna i Saha,

O     spełniony jest warunek quasi-neutralności plazmy,

O     plazmę można traktować jako gaz doskonały, tzn. można stosować do niej prawo Clapeyrona-Daltona[6].

                  Z badań eksperymentalnych wynika, że stworzenie warunków LRT w plazmie argonowej (czystej lub z domieszkami) jest możliwe w zakresie średnich i większych wartości koncentracji elektronów osiągalnych przy natężeniach prądu rzędu kilkudziesięciu do stu amperów

Istnieją również kryteria pozwalające ocenić, czy do plazmy w danych warunkach można stosować model lokalnej równowagi termodynamicznej. Dla przykładu wg Drawina  można uważać, że plazma o temperaturze T jest w LRT, gdy koncentracja elektronów (w):

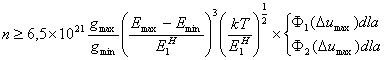
               (12)

W powyższej nierówności  odpowiada największej przerwie energetycznej w systemie poziomów energetycznych danego atomu lub jonu,  i  są wagami statystycznymi odpowiednich poziomów,  jest energią pierwszego wzbudzonego poziomu atomu wodoru, a funkcje  i  są stablicowane w pracy[7].

                  Przyjmując, że plazmę można traktować jako gaz doskonały w LRT można skorzystać z podstawowych praw termodynamiki statystycznej (z wyjątkiem prawa Plancka). Otrzymuje się wówczas układ równań, w których niewiadomymi są koncentracje składników i temperatura plazmy, a parametrami  z doświadczenia ciśnienie całkowite plazmy (atmosferyczne) oraz współczynniki emisji linii spektralnych.

Taki układ dla diagnostyki plazmy złożonej z argonu, dwutlenku węgla i wodoru może być zestawiony następująco:

                              (13)

                                                                       (14)    

                                                                               (15)

                                                                                  (16)

                                                                                  (17) 

                                                                                (18)

                                                                                  (19)

                                                                                     (20)

                                                                                     (21)

                                                                                    (22)

przy czym:

                ,                                           (23)

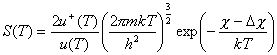               ,                              (24)

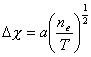                ,                                                                     (25)

gdzie:

          - natężenia linii widmowych,

         - koncentracje składników plazmy,

        p - ciśnienie całkowite,

      - obniżenie energii jonizacji na skutek zaburzenia poziomów 

             energetycznych atomu lub jonu w polu elektrycznym plazmy,

    "+"- oznacza jednokrotną jonizację.

W tym układzie równań niewiadomymi są koncentracje składników i temperatura, natomiast ciśnienie i natężenia linii są mierzalne[8].

4.1. Wyznaczanie temperatury i koncentracji elektronów.

                  W wielu przypadkach kompletna diagnostyka plazmy złożonej pod względem chemicznym jest niepotrzebna, bardzo często wystarcza tylko znajomość temperatury i koncentracji elektronów.

                  Jeśli można zmierzyć natężenie kilku linii badanego pierwiastka w tym samym stanie jonizacyjnym, wtedy można wyznaczyć temperaturę z tzw. wykresu Boltzmanna. Przekształcając równanie:

                                                             (26)

uzyskuje się wyrażenie:

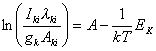             ,                                                          (27)

gdzie:

       A - współczynnik kierunkowy prostej.

Odkładając 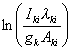   w funkcji  uzyskuje się prostą z nachylenia której otrzymuje się wartość temperatury. Warunkiem stosowalności tej metody jest to, aby występowały duże różnice w wartościach użytych linii[8].

                  Z jeszcze większą dokładnością można wyznaczyć temperaturę plazmy, gdy występują linie tego samego pierwiastka w różnych stanach jonizacyjnych. Wtedy na podstawie stosunku ich natężeń:

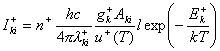                     ,                                    (28)

                  ,                                         (29)

czyli:

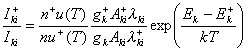                                                    (30)

oraz równania Saha - Eggerta

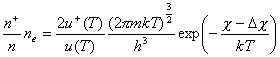                                             (31)

można wyznaczyć temperaturę.

Koncentrację elektronów można wyznaczyć korzystając z równania:

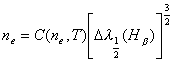                                                                    (32)

gdzie:

- stała znana z literatury,

 - szerokość połówkowa linii wodorowej l=4861,332A.[8]

Metoda ta została wykorzystana do diagnostyki plazmy w tej pracy.

 5. Parametry określające przejścia elektronów w atomie.

                  Procesy emisji i pochłaniania w szczególności charakteryzuje się przez podanie odpowiednich prawdopodobieństw przejść. Wielkości te definiuje się przy założeniu, że zmiany energii atomowych układów następują nieskończenie szybko, przypadkowo i niezależnie.

5.1. Prawdopodobieństwa przejść. Czas życia stanów wzbudzonych.

                  W celu zdefiniowania prawdopodobieństw przejść rozpatrzmy zbiór atomów lub molekuł znajdujących się w jednostce objętości. Cząstki tego zbioru mogą emitować lub pochłaniać fotony o częstości

                                                                                 (33)

gdzie:

 - energia górnego i dolnego poziomu.

W przypadku emisji spontanicznej liczba  fotonów emitowanych w jednostce czasu jest proporcjonalna do koncentracji atomów wzbudzonych do poziomu o energii , czyli:

Stały współczynnik proporcjonalności  równy ilości emitowanych w jednostce czasu fotonów o częstości  policzonych na jedną wzbudzoną cząstkę o energii nazwany jest prawdopodobieństwem przejścia lub współczynnikiem Einsteina dla emisji spontanicznej.

Wielkości analogiczne dla emisji wymuszonej i pochłaniania można zdefiniować w podobny sposób. Ilość fotonów emitowanych w jednostce czasu jest proporcjonalna do koncentracji atomów wzbudzonych do energii oraz do gęstości wymuszającego promieniowania , czyli

Analogicznie dla procesu pochłaniania otrzymujemy odpowiednią zależność:

                                    ,

skąd współczynnik Einsteina dla emisji wymuszonej jest równy:

                                     ,

oraz współczynnik Einsteina dla pochłaniania jest równy:

gdzie:

          - liczba fotonów o częstości emitowanych w jednostce czasu w rezultacie działania promieniowania o gęstości , tj. przy wymuszonych przejściach z górnego poziomu  na dolny ,

          - liczba fotonów o częstości  pochłanianych w jednostce czasu, w wyniku czego następują przejścia elektronów z poziomu dolnego  na poziom wyższy .

W przypadku równowagi promienistej związek między powyższymi wielkościami jest następujący:

oraz

                                   ,                                         (34)

gdzie:

     - stopnie zwyrodnienia (wagi statystyczne poziomów o energii  i .

Powyższe zależności w praktyce spektroskopowej odgrywają bardzo ważną rolę, ponieważ określenie jednej wielkości pozwala na obliczenie pozostałych.

Suma prawdopodobieństw przejść emisji spontanicznej z danego poziomu na pozostałe daje tzw. całkowite prawdopodobieństwo przejścia:

Odwrotność całkowitego prawdopodobieństwa spontanicznych przejść z danego poziomu  na dolne ,

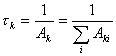
określa średni czas znajdowania się cząstki we wzbudzonym stanie. Wielkość ta nazywa się średnim czasem życia wzbudzonego stanu[4].

5.2. Wyznaczanie prawdopodobieństw przejść metodą natężeniową.

                  Korzystając z równania (2) można obliczyć prawdopodobieństwo przejścia:

                                                                  (35)

gdzie l jest długością słupa plazmy.

Jeżeli dane jest bezwzględne prawdopodobieństwo przejścia przynajmniej jednej linii danego pierwiastka, to można wyznaczyć względne prawdopodobieństwa dla innych linii drogą pomiaru natężeń tych linii. Oznaczając przez  znane, bezwzględne prawdopodobieństwo przejścia dla pewnej linii, a przez  prawdopodobieństwo przejścia dla dowolnej, innej linii tego samego pierwiastka (w tym samym stanie jonizacyjnym) można utworzyć stosunek  i z tego stosunku wyznaczyć :

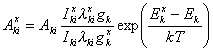                                                           (36)

                  Metoda ta jest szczególnie korzystna ze względu na to, że nie trzeba znać absolutnych natężeń linii widmowych, koncentracji składników i długości świecącej warstwy plazmy.

 6. Profile linii widmowych.

                  O profilach linii występujących w  widmie świecącej plazmy, decyduje wiele przyczyn, z których każda wnosi swoją specyfikę do kształtu profilu. W tej pracy otrzymane profile linii widmowych przybliżałem profilem Lorentza, wiec skupię się tylko nad opisem tego profilu.

6.1. Profil Lorentza.            

                 Tak różnorodne zjawiska fizyczne jak:

O     "tłumienie" przez promieniowanie, zarówno w wersji klasycznej jak                   

     i kwantowej,

O     poszerzenie linii wskutek wszelkiego rodzaju zderzeń ,

   prowadzą do rezultatów, które mogą być opisane przy pomocy dyspersyjnego wzoru Lorentza.

Otrzymany przez Lindholma rozkład natężenia promieniowania w linii  (profil linii) jest następujący:

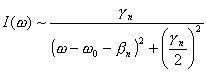                             ,                               (37)

gdzie:

          - częstość kołowa środka linii niezaburzonej.

W ramach wyprowadzonego przez Weisskopfa modelu zderzeń dalekozasięgowych występujące w powyższym wzorze wielkości mają następujący sens:

     - stała tłumienia (lub szerokość połówkowa linii w skali częstości  

           kołowej) określoną przez zderzenia silne (bliskie)

     - przesunięcie profilu względem , określonym głównie przez 

           zderzenia słabe (dalekie)

 i  zależą od rodzaju sił działających przy zderzeniach[9].

IV. Opis eksperymentu.

 1. Schemat układu pomiarowego.

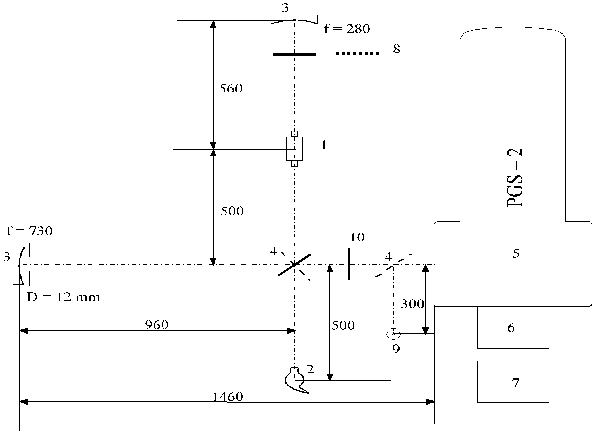
   Rys.1. Schemat układu eksperymentalnego.

  1.  Palnik kaskadowy (źródło plazmy).

  2.  Lampa wolframowa (wzorzec natężenia).

  3.  Zwierciadła wklęsłe o ogniskowych  f=730 mm i f=280 mm.

  4. Zwierciadło płaskie.

  5. Spektrograf siatkowy PGS - 2.

  6. Wielokanałowy analizator optyczny OMA - 4.

  7. Komputer.

  8. Przesłona.

  9. Lampa Plückera (wzorzec długości fali).

10. Filtr krawędziowy 450FH90.

                  Światło wychodzące z palnika (1) pada na zwierciadło płaskie (4), następnie wędruje do zwierciadła wklęsłego o ogniskowej f=730 mm i po odbiciu od niego biegnie nad lustrem (4) do spektrografu. W przypadku gdy przesłona (8) jest usunięta światło wychodzące z drugiej strony palnika po odbiciu od zwierciadła wklęsłego o ogniskowej f=280 mm wędruje z powrotem do kolumny plazmowej i po przejściu przez nią dodaje się do strumienia wiązki pierwotnej (wychodzącej bezpośrednio w kierunku zwierciadła płaskiego). Aby zarejestrować widmo lampy wolframowej należało obrócić lustro (4) o 90 stopni.

1.1. Kaskadowy palnik plazmowy jako źródło promieniowania

       elektromagnetycznego.

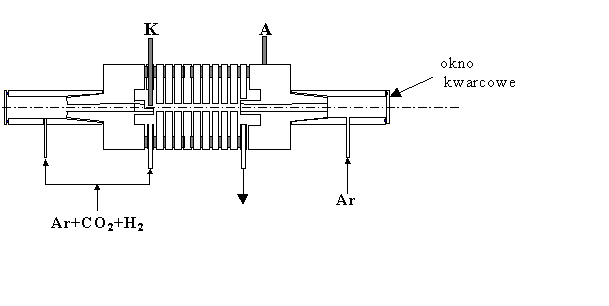Rys.2. Schemat palnika plazmowego.

                 Palnik kaskadowy składa się z pewnej liczby miedzianych krążków intensywnie chłodzonych bieżącą wodą. Każdy z nich posiada centralnie wywiercony otwór o jednakowej średnicy. Po złożeniu i oddzieleniu od siebie pierścieniami izolacyjnymi wykonanymi z teflonu uzyskujemy kanał wyładowczy o długości 6,98 cm i średnicy 4 mm. W zewnętrznych segmentach palnika są umieszczone elektrody: katoda (K) z wolframu torowego, anoda (A) z miedzi. Do przyelektrodowych części palnika wprowadzany jest czysty argon z szybkością kilkudziesięciu litrów na godzinę. Zabieg "przepłukiwania" elektrod czystym argonem znacznie polepsza stabilność pracy palnika.

                  Chcąc uzyskać widmo emisyjne węgla konieczne jest wprowadzenie do kanału wyładowczego palnika tego pierwiastka, najlepiej w postaci gazu. W tym celu do eksperymentu użyto mieszaniny następujących gazów: argonu, dwutlenku węgla oraz wodoru. Mieszanka argonu (60), dwutlenku węgla (0,6) oraz wodoru (3) była wpuszczana do palnika przy katodzie, natomiast argon o przepływie 20 był wpuszczany przy anodzie palnika tak, jak pokazuje to rys.2. Długość słupa plazmy w której znajdował się dwutlenek węgla wynosiła 69,8 mm. Kapturki z okienkami kwarcowymi zapewniały szczelność całego urządzenia. Palnik zasilany był prądem stałym o natężeniu 35 amperów.

1.2. Spektrograf, OMA - 4.

                 Urządzeniem umożliwiającym przestrzenne rozdzielenie widma w funkcji długości fali, użytym w eksperymencie był spektrograf siatkowy PGS - 2 firmy Carl - Zeiss Jena. Zmiana kąta ustawienia siatki dyfrakcyjnej realizowana przy pomocy silnika krokowego umożliwiała zmiany analizowanego fragmentu widma.

                 Urządzeniem rejestrującym widmo był wielokanałowy analizator optyczny OMA - 4 (z j. angielskiego - Optical Multichannel Analyzer). Zasadniczym elementem tego urządzenia jest płytka CCD o wymiarach  posiadająca  elementów światłoczułych o rozmiarach  każdy.

Kwanty świetlne padający na każdy taki element (nazywany dalej pikselem), powodują powstanie sygnału elektrycznego proporcjonalnego do całkowitej energii przez ten element pochłoniętej. Następnie sygnały elektryczne pochodzące z pikseli zostają zamienione na impulsy świetlne przesyłane światłowodem do komputera. W komputerze impulsy świetne zamieniane są       z powrotem na sygnały elektryczne "rozumiane" przez komputer.

1.3.Układ optyczny, rejestracja widma.

                 Odpowiednie ustawienie zwierciadeł widocznych na rys.1 oraz użycie diafragmy zapewniają, że układ odwzorowania komory palnika na szczelinie wejściowej spektrografu można traktować jako telecentryczny. Oznacza to, że urządzenie rejestrujące "widzi" jedynie te promienie świetlne, które są równoległe do osi optycznej spektrografu. Jest to konieczne z dwóch względów: po pierwsze pozwala to na porównanie natężeń źródła rozciągłego (objętościowo) jakim jest plazma wytwarzana w palniku z płaskim źródłem wzorcowym (w lampie wolframowej źródłem światła jest rozgrzana do wysokiej temperatury blaszka wolframowa). Po drugie układ taki jest konieczny ze względu na to, że plazma uzyskiwana w łuku elektrycznym jest niejednorodna przestrzennie, ma symetrię osiową. Jej temperatura jest najwyższa w obszarach przyosiowych i spada wraz z oddalaniem się od osi palnika. Układ telecentryczny pozwala na wybranie takich obszarów w plazmie, dla których temperatura i koncentracja elektronów mają w przybliżeniu jednakową wartość.

        Program dołączony do analizatora optycznego pozwala na podzielenie płytki detekcyjnej na dowolną liczbę wierszy (nie większą niż 256), przy czym każdy wiersz odpowiada za inny element plazmy. W opisywanym eksperymencie płytkę detektora podzielono na 25 wierszy nazywanych trakami ponumerowanych od 0 do 24.

        Rejestracja odbywała się jednocześnie dla wszystkich wierszy oraz dla całego przedziału widmowego obejmowanego przez płytkę detekcyjną (szerokość tego przedziału wynosiła 50 A).

                 Dla każdego przedziału widmowego dokonywano dwa zdjęcia                  z zasłoniętą przesłoną. Czas ekspozycji wynosił 0,1 sekundę. Oprócz widma plazmy rejestrowane było widmo wzorca natężenia (o czasie ekspozycji 0,1s i 10s.) oraz widmo wzorca długości fal, a także tło pomiarowe - sygnał powstały na płytce detektora pod nieobecność źródła światła (szczelina spektrografu zamknięta). Sygnał ten był następnie odejmowany od każdego zdjęcia.

V. Opracowanie wyników eksperymentu.

 1. Wstępne opracowanie plików zawierających badane widma.

                  Pierwsza część opracowania danych eksperymentalnych odbywała się w programie obsługującym OMA - 4. Składały się na to odjęcie tła pomiarowego, kalibracja czyli przypisanie poszczególnym punktom otrzymanego widma długości fali wyrażonej w angstremach oraz identyfikacja linii. Wstępnie opracowane przykładowe widmo przedstawione jest na poprzedniej stronie. Krzywe początkowe oraz końcowe (skrajne) odpowiadają za świecenie obszarów najbardziej oddalonych od osi słupa plazmy, zaś wiersze środkowe są rejestracją światła plazmy z warstw przyosiowych o najwyższej temperaturze. Widmo zawiera zarówno linie argonowe, tlenowe, jak i węglowe. Po identyfikacji czyli wyszukaniu interesujących nas linii węgla neutralnego można przystąpić do tłumaczenia plików binarnych na pliki tekstowe (kod ASCII). Dalsza część opracowania odbywała się w programie Origin 4.10.

                  Aby przejść od natężeń wyrażonych w jednostkach względnych do natężeń bezwzględnych (wyrażonych np. w jednostkach układu CGS), korzystano z widma wzorca natężenia oraz z funkcji dopasowującej do eksperymentalnie wyznaczonego natężenia lampy wolframowej. Funkcja ta daje wartości natężeń wyrażonych w jednostkach CGS i można ją stosować w przedziale długości fal od około 2500A do 24000A.

Wyraża ją wzór:

       W_L(l)= ((1,3469*10²²/l⁵)*(1/(exp(4524.5414522/l)-1))*(1+0,00211*l-

                     -(1,4074*10^-6)*l²+(2,4588*10^-10*l³)))*10⁷

        Wzór na natężenie spektralne wyrażone w jednostkach CGS wygląda następująco:

                                  ,

gdzie S(l) oraz S_L(l) są natężeniami w jednostkach względnych kolejno dla widma badanego oraz dla lampy wzorca natężenia. W_L jest natężeniem bezwzględnym obliczonym z wielomianu dopasowującego.

Otrzymane w eksperymencie profile linii widmowych przybliżano za pomocą programu Origin 4.10 profilem Lorentza. W ten sposób otrzymano dane charakteryzujące badane linie widmowe węgla, a mianowicie: maksymalne natężenie, położenie centrum linii, szerokość połówkową linii oraz poziom widma ciągłego. Przykładowe widma, które zostały opracowane za pomocą programu Origin 4.10 są przedstawione na wykresach (rys.3, rys.4.): 

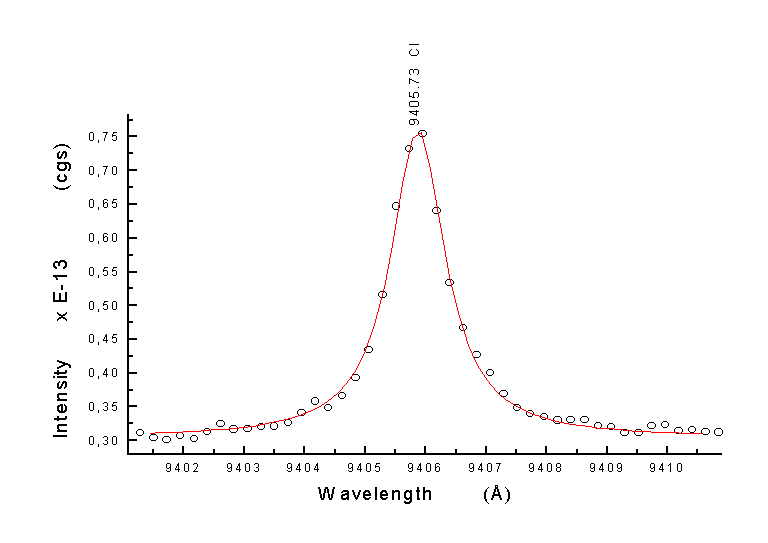             Rys.3. Linia widmowa węgla neutralnego o długości fali l=9405,73A.

 Rys.4. Linia widmowa węgla neutralnego o długości fali l=8335,15A.

                  Na poniższych wykresach przedstawiono również widma identyfikacyjne węgla neutralnego CI:

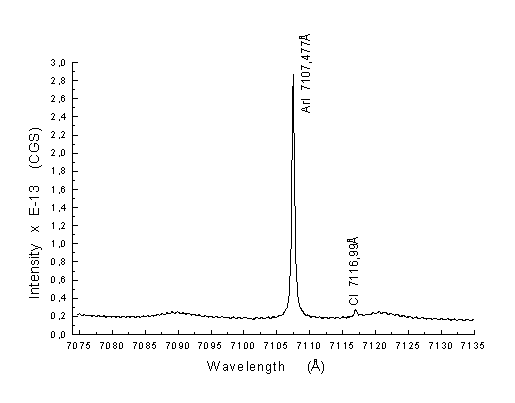
Rys.5.Linia widmowa węgla neutralnego o długości fali l=7116,99A.

Rys.6.Linia widmowa węgla neutralnego o długości fali l=8335,15A.

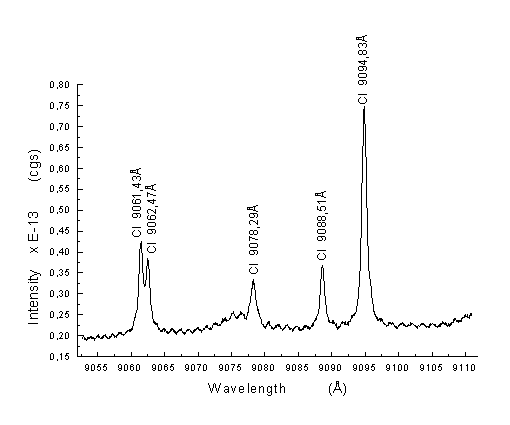
Rys.7. Linie widmowe węgla neutralnego.

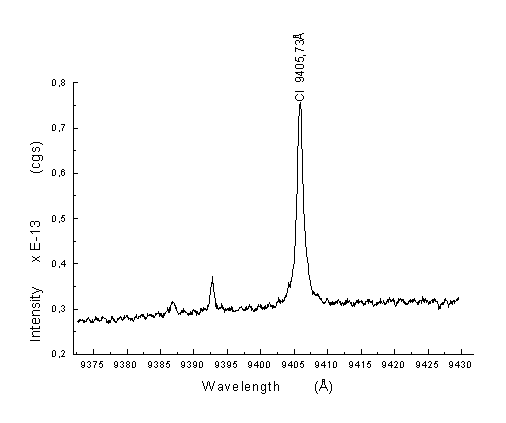
Rys.8.Linia widmowa węgla neutralnego o długości fali l=9405,73A.

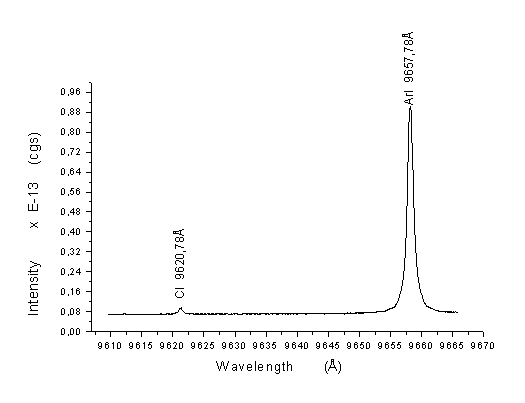
Rys.9.Linia widmowa węgla neutralnego o długości fali l=9620,78A.

 2. Sprawdzenie samoabsorpcji.

                  W celu sprawdzenia samoabsorpcji porównano natężenia badanych linii CI w maksimum (I_max) z natężeniem wynikającym z funkcji Plancka (4).

Tabela 1: Zestawienie danych do sprawdzenia samoabsorpcji plazmy.

Dalej